 Ladies, your mission is simple yet dangerous. The enemy is upon us … maybe. We have been handed a linked list. It is claimed it does not loop. But if we are to send in our troops, we better darn well make sure. Assumption is the mother of all, remember!?! It is your job to find a simple algorithm to check this linked list on loops. Ladies, O(n²) will not suffice. (Seriously, try it before reading on. Hint, the photo on the left shows Bob Floyd rendered using Floyd-Steinberg dithering.) Ladies, your mission is simple yet dangerous. The enemy is upon us … maybe. We have been handed a linked list. It is claimed it does not loop. But if we are to send in our troops, we better darn well make sure. Assumption is the mother of all, remember!?! It is your job to find a simple algorithm to check this linked list on loops. Ladies, O(n²) will not suffice. (Seriously, try it before reading on. Hint, the photo on the left shows Bob Floyd rendered using Floyd-Steinberg dithering.) |
|
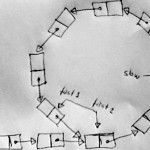 “This solution is Floyd’s Cycle-Finding Algorithm as published in Non-deterministic Algorithms by Robert W. Floyd in 1967. It is also called The Tortoise and the Hare Algorithm.“ (Stephen Ostermiller) [Finding a Loop in a Singly Linked List] “This solution is Floyd’s Cycle-Finding Algorithm as published in Non-deterministic Algorithms by Robert W. Floyd in 1967. It is also called The Tortoise and the Hare Algorithm.“ (Stephen Ostermiller) [Finding a Loop in a Singly Linked List]
Trivia: Actually this solution is not published in the above mentioned article [pdf], apparently Donald Knuth credits Floyd for the algorithm, but without citation. Since nobody influenced Knuth more than Bob Floyd [pdf], they might have simply discussed it and Knuth put it in The Art of Computer Programming II. |
Archive for August, 2010
We have all been there. Multiple threads, many objects, and than you realize you need per-object locking. Maybe you should add a mutex to each and every object, but there are many objects and collisions are rare. So, you should use a linked list with a 4-tuple node: {mutex, count, &object, &next}. Before you use an object, lock the list, see if the object is in any node: if yes, increment the count, if no, create a node with a count of 1. In either case get a pointer to the mutex and unlock the list. Now lock the node, using the pointer to the mutex and do it to the object. After which you lock the list again and either decrement the count or delete the node. Implementing that won’t be hard, just follow the doodle 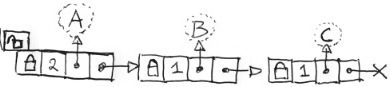 you just made while inserting imaginary objects
you just made while inserting imaginary objects A, B, A, and C (on the right). But you feel you can do better: collisions of the same object are rare but collisions of unrelated objects run rampant. You realize locking and searching the list might become a bottleneck. 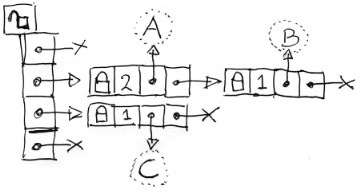 How about chopping the linked list into chunks with a hash array? You doodle some more (on the left). A little more complex, but doable. Given a large enough hash array, the list chunks will be seldom longer than one.
How about chopping the linked list into chunks with a hash array? You doodle some more (on the left). A little more complex, but doable. Given a large enough hash array, the list chunks will be seldom longer than one. ![]() Than you realize that you can give each list chunk its own mutex. And than you get that special feeling. You know the one I mean. Utter happiness hits you: Why not just fill the hash array with mutexes only? You can’t help but drawing it out (to the right), just to prolong that nice feeling. What a world, what a life, you are in love. Well, maybe not “in love” but your ventral tegmental floods your caudate with dopamine like there is no tomorrow. If you read this far, you know I am not joking.
Than you realize that you can give each list chunk its own mutex. And than you get that special feeling. You know the one I mean. Utter happiness hits you: Why not just fill the hash array with mutexes only? You can’t help but drawing it out (to the right), just to prolong that nice feeling. What a world, what a life, you are in love. Well, maybe not “in love” but your ventral tegmental floods your caudate with dopamine like there is no tomorrow. If you read this far, you know I am not joking.